Sistemas de administración y control
SACI – Sistema de Administración y Control de Inventarios, es un sistema desarrollado por Grupo Consultor en Integración de Sistemas (www.gcisnet.com.mx), el cual está enfocado al análisis de inventarios para la toma de decisiones. Este software cuenta con todas las opciones de programas Administrativos (como manejo de catálogos, compras, ventas, consignación, finanzas, etc), con la ventaja de tener integrados los conceptos de inventarios como:
- Cálculo de la demanda por medio de promedios móviles, suavizamiento exponencial simple, mínimos cuadrados).
- Clasificación del inventarios según A-B-C (Ley de pareto).- Cálculo del punto de reorden por tres categorías (A-B-C) mediante la opción de cálculo estadístico o dinámico.
- Distintos cálculos de “Sugeridos de compra”, incluyendo CEP (Cantidad Económica de Pedidos).
Modelos determinísticos
Un modelo de Optimización Matemática consiste en una función objetivo y un conjunto de restricciones en la forma de un sistema de ecuaciones o inecuaciones. Los modelos de optimización son usados en casi todas las áreas de toma de decisiones, como en ingeniería de diseño y selección de carteras financieras de inversión.
Los problemas de toma de decisiones se pueden clasificar en dos categorías: modelos de decisión determinísticos y modelos de decisión probabilísticos. En los modelos deterministicos, las buenas decisiones se basan en sus buenos resultados. Se consigue lo deseado de manera "deterministica", es decir, libre de riesgo. Esto depende de la influencia que puedan tener los factores no controlables, en la determinación de los resultados de una decisión y también en la cantidad de información que el tomador de decisión tiene para controlar dichos factores.
Aquellos que manejan y controlan sistemas de hombres y equipos se enfrentan al problema constante de mejorar (por ejemplo, optimizar) el rendimiento del sistema. El problema puede ser reducir el costo de operación y a la vez mantener un nivel aceptable de servicio, utilidades de las operaciones actuales, proporcionar un mayor nivel de servicio sin aumentar los costos, mantener un funcionamiento rentable cumpliendo a la vez con las reglamentaciones gubernamentales establecidas, o "mejorar" un aspecto de la calidad del producto sin reducir la calidad de otros aspectos. Para identificar la mejora del funcionamiento del sistema, se debe construir una representación sintética o modelo del sistema físico, que puede utilizarse para describir el efecto de una variedad de soluciones propuestas.
Un modelo puede considerarse como una entidad que captura la esencia de la realidad sin la presencia de la misma. Una fotografía es un modelo de la realidad ilustrada en la imagen. La presión arterial puede utilizarse como un modelo de la salud de una persona. Una campaña piloto de ventas puede utilizarse como un modelo de la respuesta de las personas a un nuevo producto. Por último, una ecuación matemática puede utilizarse como un modelo de la energía contenida en un determinado material. En cada caso, el modelo captura algún aspecto de la realidad que intenta representar.
Ya que un modelo sólo captura determinados aspectos de la realidad, su uso puede no ser apropiado en una aplicación en particular porque no captura los elementos correctos de la realidad. La temperatura es un modelo de las condiciones climáticas pero puede ser inapropiado si uno está interesado en la presión barométrica. Una foto de una persona es un modelo de la misma pero brinda poca información acerca de sus logros académicos. Una ecuación que predice las ventas anuales de un producto en particular es un modelo de ese producto pero tiene poca utilidad si lo que nos interesa es el costo de producción por unidad. Por lo tanto, la utilidad del modelo depende del aspecto de la realidad que representa.
Un modelo puede ser inadecuado aun cuando intenta capturar los elementos apropiados de la realidad si lo hace de una manera distorsionada o sesgada. Una ecuación que pronostica el volumen mensual de ventas puede ser exactamente lo que el gerente de ventas quiere pero podría generar grandes pérdidas si arroja constantemente cálculos de ventas altos. Un termómetro que lee de más (o de menos) tendría poca utilidad para realizar un diagnóstico médico. En consecuencia, un modelo útil es aquel que captura los elementos adecuados de la realidad con un grado aceptable de precisión.
Un modelo matemático es una ecuación, desigualdad o sistema de ecuaciones o desigualdades, que representa determinados aspectos del sistema físico representado en el modelo. Los modelos de este tipo se utilizan en gran medida en las ciencias físicas, en el campo de la ingeniería, los negocios y la economía.
Un modelo ofrece al analista una herramienta que puede manipular en su análisis del sistema en estudio, sin afectar al sistema en sí. Por ejemplo, supóngase que se ha desarrollado un modelo matemático para predecir las ventas anuales como una función del precio de venta unitario. Si se conoce el costo de producción por unidad, se pueden calcular con facilidad las utilidades anuales totales para cualquier precio de venta. Para determinar el precio de venta que arrojará las utilidades totales máximas, se pueden introducir en el modelo distintos valores para el precio de venta, uno a la vez, determinando las ventas resultantes y calculando las utilidades anuales totales para cada valor de precio de venta examinado. Mediante un proceso de prueba y error, el analista puede determinar el precio de venta que maximizará las utilidades anuales totales.
Lo ideal sería que si el modelo matemático es una representación válida del rendimiento del sistema, mediante la aplicación de las técnicas analíticas adecuadas, la solución obtenida a partir del modelo debería ser también la solución para el problema del sistema. Así, la efectividad de los resultados de la aplicación de cualquier técnica operativa es en gran medida una función del grado en el cual el modelo representa al sistema en estudio.
A fin de definir las condiciones que nos conducirán a la solución del problema del sistema, el analista primero debe identificar un criterio según el cual se podrá medir el sistema. Este criterio a menudo se denomina medida del rendimiento del sistema o medida de efectividad. En aplicaciones empresariales, la medida de efectividad generalmente son los costos o las utilidades, mientras que en aplicaciones gubernamentales esta medida generalmente se define en términos de un índice costo/beneficio.
El modelo matemático que describe el comportamiento de la medida de efectividad se denomina función objetivo. Si la función objetivo es describir el comportamiento de la medida de efectividad, debe capturar la relación entre esa medida y aquellas variables que hacen que dicha medida fluctúe. Las variables del sistema pueden categorizarse en variables de decisión y parámetros. Una variable de decisión es una variable que puede ser directamente controlada por el decisor. También existen algunos parámetros cuyos valores pueden ser inciertos para el decisor. Esto requiere un análisis de sensibilidad después de descubrir la mejor estrategia. En la práctica, resulta casi imposible capturar la relación precisa entre todas las variables del sistema y la medida de efectividad a través de una ecuación matemática. En cambio, el analista de IO/CA debe tratar de identificar aquellas variables que afectan en mayor grado la medida de efectividad y luego debe intentar definir de manera lógica la relación matemática entre estas variables y la medida de efectividad. Esta relación matemática es la función objetivo que se emplea para evaluar el rendimiento del sistema en estudio.
La formulación de una función objetivo que tenga sentido normalmente es una tarea tediosa y frustrante. Los intentos de desarrollo de una función objetivo pueden terminar en un fracaso. Esto puede darse porque el analista elige el conjunto incorrecto de variables para incluir en el modelo o bien, si el conjunto es el adecuado, porque no identifica correctamente la relación entre estas variables y la medida de efectividad. En un nuevo intento, el analista trata de descubrir las variables adicionales que podrían mejorar su modelo descartando aquellas que parecen tener poca o ninguna relevancia. No obstante, sólo se puede determinar si estos factores realmente mejoran el modelo una vez realizadas la formulación y prueba de nuevos modelos que incluyan las variables adicionales. Todo el proceso de selección y rechazo de variables puede requerir reiteraciones múltiples hasta desarrollar una función objetivo satisfactoria. En cada iteración, el analista espera lograr alguna mejora en el modelo, aunque no siempre se tiene tanta buena suerte. Por lo general, el éxito final es precedido por una serie de fracasos frustrantes y pequeños progresos.
En cada etapa del proceso de desarrollo, el analista debe evaluar la correspondencia o validez del modelo. Normalmente se emplean dos criterios para realizar esta determinación. El primero implica la experimentación del modelo: someter el modelo a una serie de condiciones y registrar los valores asociados de la medida de efectividad dada por el modelo en cada caso. Si la medida de efectividad varía de manera antinatural con una sucesión de condiciones de entrada, es posible que la función objetivo no sea válida. Por ejemplo, supóngase que se desarrolla un modelo destinado a calcular el valor de mercado de viviendas unifamiliares. El modelo debe expresar el valor de mercado en dólares como una función de la superficie cubierta en pies cuadrados, cantidad de dormitorios, cantidad de baños y tamaño del lote. Después de desarrollar el modelo, el analista lo aplica a la tasación de distintas viviendas, con distintos valores para las características mencionadas y descubre que el valor de mercado desciende a medida que aumenta la superficie cubierta expresada en pies cuadrados. Dado que este resultado no concuerda con la realidad, el analista cuestionaría la validez del modelo. Por otro lado, supóngase que el modelo es tal que el valor de las viviendas es una función creciente de cada una de las cuatro características citadas, como generalmente es de esperar. Si bien este resultado es alentador, no necesariamente implica que el modelo es una representación válida de la realidad, dado que la tasa de aumento de cada variable puede ser excesivamente alta o baja. La segunda etapa de la validación del modelo requiere una comparación de los resultados del modelo con los resultados obtenidos en la realidad.
LOTE ECONÓMICO
Es aquel pedido que optimiza los costos de pedido, almacenaje y ruptura.
El Lote Económico es aquella cantidad de unidades que deben solicitarse al proveedor en cada pedido, de manera que se logre minimizar el costo asociado a la compra y al mantenimiento de las unidades en inventario. El objetivo básico que se persigue al determinar el Lote Económico es la reducción de costos, a la vez que se responden dos preguntas claves:
• ¿Cuánto pedir?
• ¿Cuándo pedir?Para determinar el lote económico debemos identificar cuáles son los costos asociados a los inventarios:
1. COSTOS DE COLOCACION DEL PEDIDO C1: Este valor se considera fijo cualquiera sea la cuantía del lote, pues no están afectados por el tipo de políticas de inventarios. Está representado por el costo del formato de compra, tiempo de computador, el costo de enviar la orden de compra al proveedor, etc.
2. COSTOS DE MANTENIMIENTO/UNID DE TIEMPO C2: Se define como el costo de mantener una unidad o artículo durante un tiempo determinado. Los artículos que se almacenan en inventario, además están sujetos a pérdidas por robo, obsolescencia y deterioro.
3. COSTOS DE QUEDARSE CORTO: Cuando una empresa por cualquier circunstancia no puede cumplir un pedido, por lo general ocurren dos comportamientos, que dan lugar a dos tipos de costos:
3.1 Costos de ruptura C3: Está representado por la falta de un artículo durante un tiempo determinado. La característica principal es que a pesar del incumplimiento, el cliente prefiere esperar.
3.2 Costos de Faltantes C4: Está representado por la falta de un artículo durante un tiempo determinado. En este caso la demanda no es cautiva, se pierde la venta y se pierde el cliente.
4. COSTOS DE SOBRANTES C5: Este costo es causado por deterioro, obsolescencia, inversión inoficiosa e inutilidad de un artículo o material cuando no es utilizado antes de determinado tiempo.
Como conclusión podemos decir que:
Dentro de las funciones principales de una empresa está la producción y para lograr una gestión eficaz conviene que los responsables de dicha gestión elaboren un plan de trabajo ya que se trata de conseguir el mejor aprovechamiento de los medios disponibles para las tareas relativas a compra, almacenaje, stock de materias primas, modelos de gestión de inventarios, el nivel de stock de seguridad entre otros. Dichos medios se valen de una preparación administrativa y técnica de los trabajos.
En concordancia, con las consideraciones antes mencionadas para finalizar se puede decir que:
• La gerencia de la empresa, el empresario debe formar parte de esta programación.• Asegurar la perfecta y adecuada utilización de los medios de producción disponibles con el fin de obtener los costes de producción más reducidos posibles.
• Prever las necesidades en materias primas, elementos para montaje, en personal y en inventario de todo tipo para obtener la producción establecida.
• Garantizar la cobertura total de las necesidades de la empresa al objeto de que los stocks de materias primas y de elementos para montaje, dentro de los límites tales que representen un margen de seguridad en el aprovisionamiento a los talleres de elaboración.
LOTE ECONÓMICO CON DEFICIT
El volumen óptimo de pedido o lote económico de compra es aquella cantidad que la empresa debe pedir a sus proveedores, de forma que el coste de aprovisionamiento sea mínimo. La solución del problema en condiciones deterministas se realiza mediante el modelo de Wilson, que desarrollamos a continuación y que está compuesto por los siguientes costes:-Coste de adquisición del producto: D x P
D= Demanda o uso anual del producto
P= Precio del producto-Coste de aprovisionamiento o renovación: E D/Q
E=Coste de encargo o coste de preparación del pedido realizado
Q=Volumen de pedido o cantidad que se ha de encargar cada vez
-Coste de almacenamiento: [A+(Pxi)]Q
A: Coste de almacenamiento de una unidad de producto durante un año
I: Tipo de interés (coste de capital)
La función de Costes Totales será la suma de los componentes anteriores:
CT=DxP+(ExD/Q)+ [A+(Pxi)]Q, desarrollando obtendríamos: Q=√(█(2ED@[A+(Pxi) ] ))Por lo tanto, se ha de hacer el pedido cuando las existencias en el almacén sean suficientes para atender la demanda durante el plazo de reposición. Denominamos “punto de pedido” al nivel de existencias que define el momento en el que se ha de efectuar el pedido.
Ejemplo:
Supongamos que una empresa adquiere sus materias primas a un coste de 0,15 € por unidad. La empresa necesita anualmente 140.000 unidades. Por cada pedido realizado, la empresa estima, en concepto de gastos administrativos, transporte y descarga, un coste de 60,10 € y el tiempo promedio en recibir el pedido desde que se efectúa es de 15 días. Con los datos de la contabilidad hemos calculado que cada unidad de producto almacenado supone un coste anual de 0,01 € . Sabiendo que el coste de capital en la empresa es de 12%, se desea conocer el volumen económico de pedido. ¿Cada cuánto tiempo se debe realizar un pedido y cuál es el punto de pedido?
- La función de costes totales de almacenamiento y adquisición es:
140.000 0,01+ 0,15 x 0,12
CT = 140.000 x 0,15 + 60,10 –––––––– + –––––––––––––– x Q
Q 2Aplicando la fórmula del volumen económico de pedido obtenida anteriormente, obtenemos la cantidad “Q” que se ha de encargar en cada pedido:
2ED 2(60,10)(140.000)
Q = –––––––––– = ––––––––––––––––– = 2.887,7 unidades
[A + (P 5 i)] 2 + (0,15 5 0,12)El tiempo que transcurre entre cada pedido será el número de días de demanda que cubre la citada cantidad. Si suponemos que la empresa trabaja 300 días al año, el consumo diario será:
140.000 unidades demandadas en un año
–––––––––––––––––––––––––––––––––– = 466,66 unidades diarias
300 días de trabajo
Y por consiguiente, el tiempo “T” que transcurre entre cada pedido será:
Volumen económico de pedido 2.887,7
––––––––––––––––––––––––– = –––––– = 6.18 días
Consumo diario 466,66
En consecuencia, la empresa deberá encargar un nuevo pedido cuando queden existencias suficientes para 15 días (plazo de entrega). La cantidad existente en almacén o punto de pedido “r” será igual al plazo de entrega por el consumo diario:
r = 15 x 466,66 = 7.000 unidadesLOTE ECONÓMICO DE PRODUCCION
Es aquel pedido que optimiza los costos de pedido, almacenaje y ruptura.
El Lote Económico es aquella cantidad de unidades que deben solicitarse al proveedor en cada pedido, de manera que se logre minimizar el costo asociado a la compra y al mantenimiento de las unidades en inventario. El objetivo básico que se persigue al determinar el Lote Económico es la reducción de costos, a la vez que se responden dos preguntas claves:
• ¿Cuánto pedir?
• ¿Cuándo pedir?
Para determinar el lote económico debemos identificar cuáles son los costos asociados a los inventarios:
1. COSTOS DE COLOCACION DEL PEDIDO C1: Este valor se considera fijo cualquiera sea la cuantía del lote, pues no están afectados por el tipo de políticas de inventarios. Está representado por el costo del formato de compra, tiempo de computador, el costo de enviar la orden de compra al proveedor, etc.
2. COSTOS DE MANTENIMIENTO/UNID DE TIEMPO C2: Se define como el costo de mantener una unidad o artículo durante un tiempo determinado. Los artículos que se almacenan en inventario, además están sujetos a pérdidas por robo, obsolescencia y deterioro.
3. COSTOS DE QUEDARSE CORTO: Cuando una empresa por cualquier circunstancia no puede cumplir un pedido, por lo general ocurren dos comportamientos, que dan lugar a dos tipos de costos:
3.1 Costos de ruptura C3: Está representado por la falta de un artículo durante un tiempo determinado. La característica principal es que a pesar del incumplimiento, el cliente prefiere esperar.
3.2 Costos de Faltantes C4: Está representado por la falta de un artículo durante un tiempo determinado. En este caso la demanda no es cautiva, se pierde la venta y se pierde el cliente.
4. COSTOS DE SOBRANTES C5: Este costo es causado por deterioro, obsolescencia, inversión inoficiosa e inutilidad de un artículo o material cuando no es utilizado antes de determinado tiempo.
El cálculo del Lote Económico pude obtenerse a través de la aplicación de modelos matemáticos, cada uno de los cuales utiliza ciertos supuestos. Algunos de estos modelos son:
Probabilistico | | Demanda Flexible |
| | Suministro Incierto |
Deterministico | | Demanda Constante |
| | Suministro Instantáneo |
Vamos a calcular el tamaño del lote a través de la aplicación del modelo Determinístico de Harris:
Alternativa 1
Alternativa 2Alternativa N
De las gráficas anteriores, se puede deducir:
• Si T es grande, q (tamaño del lote) también lo es y el costo de almacenamiento es grande. En cambio n es pequeño, pues hay que hacer pocos pedidos.
• Si T es pequeño, q (tamaño del lote) también lo es y el costo de almacenamiento es pequeño. En cambio n es grande, pues hay que hacer muchos pedidos.
MODELO DE TAMAÑO DEL LOTE ECONÓMICO BÁSICO (EOQ)
Esta técnica es relativamente fácil de usar pero hace una gran cantidad de suposiciones. Las más importantes son:
1. La demanda es conocida y constante
2. El tiempo de entrega, esto es, el tiempo entre la colocación de la orden y la recepción del pedido, se conoce y es constante.
3. La recepción del inventario es instantánea. En otras palabras, el inventario de una orden llega en un lote el mismo momento.
4. Los descuentos por cantidad no son posibles.
5. Los únicos costos variables son el costo de preparación o de colocación de una orden (costos de preparación) y el costo del manejo o almacenamiento del inventario a través del tiempo (costo de manejo).
6. Las faltas de inventario (faltantes) se pueden evitar en forma completa, si las órdenes se colocan en el momento adecuado.
Variables del modelo:
Q = número de piezas por orden.
Q* = número óptimo de piezas por orden (EOQ).
D = demanda anual en unidades para el producto del inventario.
S = costo de preparación para cada orden.
H = costo de manejo del inventario por unidad por año.
N = número esperado de órdenes.
T = tiempo esperado de órdenes.
CT = costo total.
UNIDAD 5
Líneas de espera.
Introducción
Definiciones, características y suposiciones.
El problema es determinar que capacidad o tasa de servicio proporciona el balance correcto. Esto no es sencillo, ya que el cliente no llega a un horario fijo, es decir, no se sabe con exactitud en que momento llegarán los clientes. También el tiempo de servicio no tiene un horario fijo.
Definición.
Una Cola es una línea de espera y la teoría de colas es una colección de modelos matemáticos que describen sistemas de líneas de espera particulares o sistemas de colas. Los modelos sirven para encontrar el comportamiento de estado estable, como la longitud promedio de la línea y el tiempo de espera promedio para un sistema dado. Esta información, junto con los costos pertinentes, se usa, entonces, para determinar la capacidad de servicio apropiada.
Costos de los sistemas de colas.
Un sistema de colas puede dividirse en sus dos componentes de mayor importancia, la cola y la instalación de servicio . Las llegadas son las unidades que entran en el sistema para recibir el servicio. Siempre se unen primero a la cola; si no hay línea de espera se dice que la cola esta vacía . De la cola, las llegadas van a la instalación de servicio de acuerdo con la disciplina de la cola, es decir, de acuerdo con la regla para decidir cuál de las llegadas se sirve después. El primero en llegar primero en ser servido es una regla común, pero podría servir con prioridades o siguiendo alguna otra regla. Una vez que se completa el servicio, las llegadas se convierten en salidas.
Ambas componentes del sistema tienen costos asociados que deben de considerarse.
Costo de Espera.
Esperar significa desperdicio de algún recurso activo que bien se puede aprovechar en otra cosa y esta dado por :
Costo total de espera = CwL
Donde Cw = costo de espera por hora (en dólares) por llegada por unidad de tiempo y L= longitud promedio de la línea.
Costo de Servicio.
Este en la mayoría se trata de comprar varias instalaciones de servicio , en estos casos solo se ocupan los costos comparativos o diferenciales.
Sistema de costo mínimo.
Aquí hay que tomar en cuenta que para tasas bajas de servicio, se experimenta largas colas y costos de espera muy altos. Conforme aumenta el servicio disminuyen los costos de espera, pero aumenta el costo de servicio y el costo total disminuye, sin embargo , finalmente se llega a un punto de disminución en el rendimiento. Entonces el propósito es encontrar el balance adecuado para que el costo total sea el mínimo.
Estructuras típicas.
Las llegadas pueden ser personas, cartas, carros, incendios, ensambles intermedios en una fábrica, etc. En la siguiente tabla se muestran algunos ejemplos de varios sistemas de colas.
Ejemplos de sistemas de colas
| Situación | Llegadas | Cola | Mecanismo de Servicio |
| Aeropuerto | Aviones | Aviones en carreteo | Pista |
| Aeropuerto | Pasajeros | Sala de espera | Avión |
| Depto de bomberos | Alarmas de incendio | Incendios | Depto. De Bomberos. |
| Compañía telefónica | Números marcados | Llamadas | Conmutador |
| Lavado de carros | Autos | Autos sucios | Mecanismo de lavado |
| La corte | Casos | Casos atrasados | Juez |
| Panadería | Clientes | Clientes con números | Vendedor |
| Carga de camiones | Camiones | Camiones en espera | Muelle de carga |
| Oficina de correos | Cartas | Buzón | Empleados por correos |
| Crucero | Autos | Autos en línea | Crucero |
| Fábrica | Subensamble | Inventario en proceso | Estación de trabajo. |
| Cartas de negocios | Notas de dictado | Cartas para mecanografiar | Secretaria |
| Reproducción | Pedidos | Trabajos | Copiadoras |
| Hospital | Pacientes | Personas enfermas | Hospital |
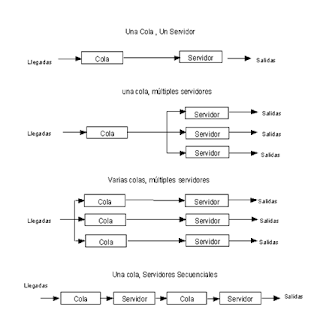
Permitiendo que varíen el número de colas y el número de servidores, pueden hacerse los diagramas de los cuatro tipos de sistemas de la siguiente figura. Cada línea de espera individual y cada servidor individual se muestra por separado.
El primer sistema que se muestra en la figura, se llama un sistema de un servidor y una cola o puede describir un lavado de carros automático o un muelle de descarga de un solo lugar. El segundo, una línea con múltiples servidores, es típico de una peluquería o una panadería en donde los clientes toman un número al entrar y se les sirve cuando llega el turno. El tercer sistema, aquél en que cada servidor tiene una línea de separada, es característico de los bancos y las tiendas de autoservicio. El cuarto sistema, es una línea con servidores en serie, puede describir una fábrica.
Terminología Notación Líneas de Espera
Estos son algunos conceptos que se utilizan en los modelos de líneas de espera:
DISCIPLINA DE SERVICIO: La disciplina de servicio se refiere al orden en el que se seleccionan los clientes de la cola para recibir el servicio. Por ejemplo, puede ser:
PEPS (Primero en Entrar Primero en Salir, también conocida como FIFO: first in firstout) primero en entrar, primero en salir, según la cual se atiende primero al cliente que haya llegado de primero. UEPS (Ultimo en Entrar Primero en Salir, también conocida como LIFO: last in firstout) también se conoce como pila, consiste en atender primero al cliente que ha llegado de último.
SOA (Servicio en Orden Aleatorio, también se conoce como SIRO o RSS: randomselection of service) que selecciona los clientes de manera aleatoria, de acuerdo a algún procedimiento de prioridad o a algún otro orden. PRIORIDAD en el servicio: Los clientes se atienden de primero de acuerdo a alguna prioridad especificada. Si se forma alguna cola con prioridad, seguirá alguna disciplina de servicio.
Procesamiento equilibrado o igualitario, también llamado ProcessorSharing: Sirve a todos los clientes por igual. La capacidad del sistema se comparte entre los clientes y todos experimentan el mismo retraso.
TERMINOLOGÍA Y NOTACIÓN:
No se permite el faltante. Suposiciones:
1. La demanda tiene que ser constante.
2. Los costos son constantes (no se permite descuento en adquisiciones voluminosas).
3. Los proveedores entregaran con puntualidad los pedidos en el periodo comprendido.
4. El lote mínimo es igual al inventario máximo.
Nomenclatura:
Q = tamaño económico del lote. Si es muy grande o muy chico
N = número de pedido. Puedes pedir una o 2 veces
D = Demanda. Por si las dudas ten cuidado y siempre papelito habla Ci = Costo de compra. A lo mejor te sale mas barato en otro lado
Ch = Costo de mantener un unidad en los inventarios (%). Co = Costo de ordenar. Ya ves que hay gandallas que te cobran el envió
R = Punto de reorden. L = Tiempo de consumo. En menos de 30 min si te cobran sino PS no
T = Tiempo para consumir el inventario máximo. el tiempo en el que te atragantas
Imáx = Inventario Máximo.
Î =Inventario Promedio.
Ct = Costo Total.
Ct = Costo de compra + Costo de ordenar + Costo de tenencia.
Costo de compra = CiD
Proceso de nacimiento o muerte
Este informe tiene como finalidad presentar una teoría operacional sobre la Teoría de Colas, la cual incluye el estudio matemático de las colas o líneas de espera, siendo la de mayor aplicación potencial y sin embargo es la más difícil de aplicar. Los fenómenos de espera para recibir servicio son cosas de la vida diaria; por ejemplo, esperar en una cola para pagar el teléfono o en el supermercado. No obstante, la espera no solo se limita a personas sino a procedimientos o ensamblados de máquinas, por lo tanto en esta unidad se describen modelos matemáticos aplicables a cualquier situación donde se forme una cola.No pretendo incluir en un solo tema todo lo que necesita saber el estudiante, sino ofrecer un marco de los conocimientos básicos presentados en forma clara y precisa.
La formación de líneas de espera es, por supuesto, un fenómeno común que ocurre siempre que la demanda actual de un servicio excede a la capacidad actual de proporcionarlo. Con frecuencia, en la industria y en otros sitios, deben tomarse decisiones respecto a la cantidad de capacidad que debe proporcionarse. Sin embargo, muchas veces es imposible predecir con exactitud cuándo llegarán las unidades que buscan el servicio y/o cuánto tiempo será necesario para dar ese servicio; es por esto que esas decisiones suelen ser difíciles. Proporcionar demasiado servicio implica costos excesivos. Por otro lado, carecer de la capacidad de servicio suficiente causa colas excesivamente largas en ciertos momentos. Las líneas de espera largas también son costosas en cierto sentido, ya sea por un costo social, por un costo causado por la pérdida de clientes, por el costo de empleados ociosos o por algún otro costo importante. Entonces, la meta final es lograr un balance económico entre el costo de servicio y el costo asociado con la espera por ese servicio. La teoría de colas en sí no resuelve directamente este problema, pero contribuye con información vital que se requiere para tomar las decisiones concernientes prediciendo algunas características sobre la línea de espera como el tiempo de espera promedio.
La teoría de colas proporciona un gran número de modelos matemáticos para describir una situación de línea de espera. Con frecuencia se dispone de resultados matemáticos que predicen algunas de las características de estos modelos.
Como ejemplo prototipo expondré la sala de emergencia del Hospital General, el cual proporciona cuidados médicos rápidos a los casos de emergencia que llegan en ambulancia o vehículos particulares. En cualquier momento se cuenta con un doctor de guardia. No obstante, a causa de la mala situación económica que vive nuestro país existe una creciente tendencia a usar estas instalaciones para casos de emergencia en lugar de ir a una clínica privada, es por ello que el hospital ha venido experimentando un aumento continuo en el número de pacientes anuales que llegan a la sala de emergencia. Como resultado, es bastante común que los pacientes que llegan durante las horas pico (temprano en la tarde) tengan que esperar turno para recibir el tratamiento del doctor. Por esto, se ha hecho una propuesta para asignar un segundo doctor a la sala de emergencia durante esas horas pico, para que se puedan atender dos casos de emergencia al mismo tiempo. Se ha pedido al ingeniero administrador del hospital que estudie esta posibilidad.
El ingeniero comenzó por reunir los datos históricos pertinentes y por hacer una proyección de estos datos al siguiente año. Reconoció que la sala de emergencia es un sistema de líneas de espera y aplicó algunos modelos de teoría de colas para predecir las características de la espera en el sistema con uno y dos doctores como veremos a continuación:
ESTRUCTURA BÁSICA DE LOS MODELOS DE COLAS
Proceso básico de colas
El proceso básico supuesto por la mayor parte de los modelos de colas es el siguiente. Los clientes que requieren un servicio se generan a través del tiempo en una fase de entrada. Estos clientes entran al sistema y se unen a una cola. En determinado momento se selecciona un miembro de la cola, para proporcionarle el servicio, mediante alguna regla conocida como disciplina de servicio. Luego, se lleva a cabo el servicio requerido por el cliente en un mecanismo de servicio, después de lo cual el cliente sale del sistema de colas. En la siguiente figura se da un esquema de este proceso.Fuente de entrada (población potencial)
Una característica de la fuente de entrada es su tamaño. El tamaño es el número total de clientes que pueden requerir servicio en determinado momento, es decir, el número total de clientes potenciales distintos. Esta población a partir de la cual surgen las unidades que llegan se conoce como población de entrada. Puede suponerse que el tamaño es infinito o finito (de modo que también se dice que la fuente de entrada es ilimitada o limitada). Como los cálculos son mucho más sencillos para el caso infinito, esta suposición se hace muy seguido aun cuando el tamaño real sea un número fijo relativamente grande, y deberá tomarse como una suposición implícita en cualquier modelo que no establezca otra cosa. El caso finito es más difícil analíticamente, pues el número de clientes en la cola afecta el número potencial de clientes fuera del sistema en cualquier tiempo; pero debe hacerse esta suposición finita se la tasa a la que la fuente de entrada genera clientes nuevos queda afectada en forma significativa por el número de clientes en el sistema de líneas de espera.
También se debe especificar el patrón estadístico mediante el cual se generan los clientes a través del tiempo. La suposición normal es que se generan de acuerdo a un proceso Poisson, es decir, el número de clientes que llegan hasta un tiempo específico tiene una distribución Poisson. En nuestro caso corresponde a aquel cuyas llegadas al sistema ocurren de manera aleatoria pero con cierta tasa media fija y sin importar cuántos clientes están ya ahí (por lo que el tamaño de la fuente de entrada es infinito). Una suposición equivalente es que la distribución de probabilidad del tiempo que transcurre entre dos llegadas consecutivas es exponencial. Se hace referencia al tiempo que transcurre entre dos llegadas consecutivas como tiempo entre llegadas.
Cola
Una cola se caracteriza por el número máximo permisible de clientes que puede admitir. Las colas pueden ser finitas o infinitas, según si este numero es finito o infinito. La suposición de una cola infinita es la estándar para la mayor parte de los modelos, incluso en situaciones en las que de hecho existe una cota superior (relativamente grande) sobre el número permitido de clientes, ya que manejar una cota así puede ser un factor complicado para el análisis. Los sistemas de colas en los que la cota superior es tan pequeña que se llega a ella con cierta frecuencia, necesitan suponer una cola finita.Disciplina de la cola
La disciplina de la cola se refiere al orden en el que se seleccionan sus miembros para recibir el servicio. Por ejemplo, puede ser: primero en entrar, primero en salir, aleatoria, de acuerdo a algún procedimiento de prioridad o a algún otro orden. La que suponen como normal los modelos de colas es la primero en entrar, primero en salir, a menos que se establezca otra cosa.
Mecanismo de servicio
El mecanismo de servicio consiste en una o más instalaciones de servicio, cada una de ellas con uno o más canales paralelos de servicio, llamados servidores. Si existe más de una instalación de servicio, puede ser que sirva al cliente a través de una secuencia de ellas (canales de servicio en serie). En una instalación dada, el cliente entra en uno de estos canales y el servidor le presta el servicio completo. Un modelo de colas debe especificar el arreglo de las instalaciones y el número de servidores (canales paralelos) en cada una. Los modelos más elementales suponen una instalación, ya sea con un servidor o con un número finito de servidores.
El tiempo que transcurre desde el inicio del servicio para un cliente hasta su terminación en una instalación se llama tiempo de servicio (o duración del servicio). Un modelo de un sistema de colas determinado debe especificar la distribución de probabilidad de los tiempos de servicio para cada servidor (y tal vez para los distintos tipos de clientes), aunque es común suponer la misma distribución para todos los servidores.
Un proceso de colas elemental
Como ya se ha sugerido, la teoría de colas se aplica a muchos tipos diferentes de situaciones. El tipo que más prevalece es el siguiente: una sola línea de espera (que puede estar vacía en ciertos lapsos de tiempos) se forma frente a una instalación de servicio, dentro de la cual se encuentran uno o más servidores. Cada cliente generado por una fuente de entrada recibe servicio de uno de los servidores, quizá después de esperar un poco en la cola (línea de espera). En la figura se da un esquema del sistema de colas elemental del que se habla (cada cliente se indica por una C y cada servidor por una S ). Observe que el proceso que ilustramos en el ejemplo al inicio es de este tipo. La fuente de entrada genera clientes en la forma de casos de emergencia que requieren cuidado médico. La sala de emergencia es la instalación de servicio y los doctores son los servidores.
Un servidor no tiene que ser un solo individuo; puede ser un grupo de personas, por ejemplo, una cuadrilla de reparación que combina fuerzas para realizar, de manera simultánea, el servicio que solicita el cliente. Aún más, los servidores ni siquiera tienen que ser personas. En muchos casos puede ser una máquina o una pieza de equipo, como un cargador frontal que presta el servicio cuando se requiere (tal vez con la ayuda de un operador). Con esta misma línea de ideas, los clientes en la cola no tienen que ser personas. Por ejemplo, pueden ser unidades que esperan ser procesadas en una cierta máquina, o pueden ser carros que esperan pasar por una caseta de cobro.
No es necesario que de hecho se forme físicamente una línea de espera delante de una estructura física que constituye la instalación de servicio; es decir, los miembros de la cola pueden estar dispersos en un área mientras esperan que el servidor venga a ellos, como las máquinas que esperan reparación. El servidor o grupo de servidores asignados a un área constituyen la instalación de servicio para esa área. De todas maneras, la teoría de colas da un número promedio de clientes en espera, el tiempo promedio de espera, etc. pues es irrelevante si los clientes esperan agrupados o no. El único requisito esencial para poder aplicar la teoría de colas es que los cambios en el número de clientes que esperan un servicio ocurran como si prevaleciera la situación física que se describe en la figura anterior (o una contraparte valida).
Muchos de los modelos para la teoría de colas hacen la suposición de que todos los tiempos entre llegadas y todos los tiempos de servicio son independientes e idénticamente distribuidos. Por ejemplo, el modelo M/M/s supone que tanto los tiempos entre llegadas como los de servicio tienen una distribución exponencial y que el número de servidores es s (cualquier entero positivo). El modelo M/G/1 supone que los tiempos entre llegadas siguen una distribución exponencial pero no pone restricciones sobre la distribución de los tiempos de servicio, mientras que el número de servidores está restringido a exactamente 1.
EJEMPLOS DE SISTEMAS DE COLAS REALES
Puede parecer que la descripción de los sistemas de colas pueden parecer más o menos abstracta y sólo es aplicables en situaciones prácticas bastante especiales. Por el contrario, los sistemas de colas ocurren con sorprendente frecuencia en una amplia variedad de contextos. Para ampliar el horizonte sobre la aplicabilidad de la teoría de colas, se mencionarán brevemente varios ejemplos reales de sistemas de colas.
Una clase importante de sistemas de colas que se encuentran en la vida es el sistema de servicio comercial, en donde los clientes externos reciben un servicio de una organización comercial. Muchos de estos sistemas incluyen un servicio de persona a persona en una localidad fija, como una peluquería (los peluqueros son los servidores), es servicio de una cajera de banco, las cajas de cobro en un supermercado y una cola en una cafetería (canales de servicio en serie). Muchos otros sistemas son de tipo diferente, como la reparación de aparatos domésticos (el servidor va hacia el cliente), una maquina de monedas (el servidor es una máquina) y una gasolinera (los clientes son automóviles).
Otra clase importante es la de sistemas de servicio de transporte. Para algunos de estos sistemas los vehículos son los clientes, como los automóviles que esperan pasar por una caseta de cobro o un semáforo (el servidor), un camión de carga o un barco que esperan que una cuadrilla les dé el servicio de carga o descarga y un avión que espera aterrizar o despegar en una pista (el servidor). (Un estacionamiento es un ejemplo poco usual de este tipo, en el que los carros son los clientes y los espacios son los servidores, pero no existe una cola porque si el estacionamiento está lleno, los clientes se van a otro lado a estacionarse). En otros casos, los vehículos son los servidores, como los taxis, los camiones de bomberos y los elevadores.
En los últimos años, tal vez la teoría de colas se ha aplicado más a los sistemas de servicio interno en la industria y en los negocios, en donde los clientes que reciben el servicio son internos o parte de la organización. Los ejemplos incluyen sistemas de manejo de materiales, en donde las unidades de manejo de materiales (los servidores) mueven cargas (los clientes); sistemas de mantenimiento, en donde las brigadas de mantenimiento (los servidores) reparan máquinas (los clientes) y puestos de inspección en los que los inspectores de control de calidad (los servidores) inspeccionan artículos (los clientes). Las instalaciones para empleados y los departamentos que dan servicio a empleados también entran en esta categoría. Además, las máquinas se pueden ver como servidores cuyos clientes son los trabajos que se están procesando. Un ejemplo relacionado muy importante es un centro de cómputo en el que la computadora se puede ver como el servidor.
Es del reconocimiento general que la teoría de colas también se puede aplicar a sistemas de servicio social. Por ejemplo, un sistema judicial es una red de colas, en donde las cortes son las instalaciones de servicio, los jueces (o los jurados) son los servidores y los casos que esperan el proceso son los clientes. Un sistema legislativo es una red de colas parecida, en el que los clientes son los asuntos que el congreso va a tratar. Algunos sistemas de salud pública son sistemas de colas. Al inicio se vio un ejemplo (la sala de emergencia de un hospital), pero también las ambulancias, las máquinas de rayos X y las camas del hospital pueden jugar el papel de servidores en sus propios sistemas de colas. En forma parecida, las familias en espera de viviendas de interés social u otros servicios sociales se pueden concebir como clientes de un sistema de colas.
Aun cuando éstas son cuatro clases amplias de sistemas de colas, la lista todavía no se agota. De hecho, la teoría de colas comenzó a principios de siglo con aplicaciones a ingeniería telefónica (el fundador de la teoría de colas, A.K. Erlang, era un empleado de la Danish Telephone Company en Copenhague), y la ingeniería telefónica constituye todavía una importante aplicación. Lo que es más, cada individuo tiene sus propias líneas de espera personales: tareas, libros que leer, etc. Estos ejemplos son suficientes para sugerir que los sistemas de colas sin duda ocurren con toda frecuencia en muchas áreas de la sociedad.
PROCESO DE NACIMIENTO Y MUERTE
La mayor parte de los modelos elementales de colas suponen que las entradas (llegada de clientes) y las salidas (clientes que se van) del sistema ocurren de acuerdo al proceso de nacimiento y muerte. Este importante proceso de teoría de probabilidad tiene aplicaciones en varias áreas. Sin embrago en el contexto de la teoría de colas, el término nacimiento se refiere a llegada de un nuevo cliente al sistema de colas y el término muerte se refiere a la salida del cliente servido. El estado del sistema en el tiempo t (t 0), denotado por N (t), es el número de clientes que hay en el sistema de colas en el tiempo t. El proceso de nacimiento y muerte describe en términos probabilísticos cómo cambia N (t) al aumentar t. En general, dice que los nacimientos y muertes individuales ocurren aleatoriamente, en donde sus tasas medias de ocurrencia dependen del estado actual del sistema. De manera más precisa, las suposiciones del proceso de nacimiento y muerte son las siguientes:
SUPOSICIÓN 1. Dado N (t) = n, la distribución de probabilidad actual del tiempo que falta para el próximo nacimiento (llegada) es exponencial con parámetro (n=0,1,2,….).
SUPOSICIÓN 2. Dado N (t) = n, la distribución de probabilidad actual del tiempo que falta para la próxima muerte (terminación de servicio) es exponencial con parámetro (n=1,2,….).
SUPOSICIÓN 3. La variable aleatoria de la suposición 1 (el tiempo que falta hasta el próximo nacimiento) y la variable aleatoria de la suposición 2 (el tiempo que falta hasta la siguiente muerte) son mutuamente independientes.
Como consecuencia de las suposiciones 1 y 2, el proceso de nacimiento y muerte es un tipo especial de cadena de Markov de tiempo continuo. Los modelos de colas que se pueden representar por una cadena de Markov de tiempo continuo son mucho más manejables analíticamente que cualquier otro.
Excepto por algunos casos especiales, el análisis del proceso de nacimiento y muerte es complicado cuando el sistema se encuentra en condición transitoria. Se han obtenido algunos resultados sobre esta distribución de probabilidad de N (t) pero son muy complicados para tener un buen uso práctico. Por otro lado, es bastante directo derivar esta distribución después de que el sistema ha alcanzado la condición de estado estable (en caso de que pueda alcanzarla).
C O N C L U S I O N
Los sistemas de colas son muy comunes en la sociedad. La adecuación de estos sistemas pueden tener un efecto importante sobre la calidad de vida y la productividad.
Para estudiar estos sistemas, la teoría de colas formula modelos matemáticos que representan su operación y después usa estos modelos para obtener medidas de desempeño. Este análisis proporciona información vital para diseñar de manera efectiva sistemas de colas que logren un balance apropiado entre el costo de proporcionar el servicio y el costo asociado con la espera por ese servicio.
En este informe se realizo un resumen de algunos modelos básicos de teoría de colas para los que se tienen resultados particularmente útiles. Se hubiera podido considerar muchos otros modelos interesantes si el espacio lo hubiera permitido. De hecho, han aparecido en la literatura técnica varios miles de artículos de investigación que formulan y/o analizan modelos de colas, y ¡cada año se publican mucho más!
La distribución exponencial juega un papel fundamental en la teoría de las colas para representar la distribución de los tiempos entre llegadas y de servicio, ya que esta suposición permite representar un sistema de colas como una cadena de Markov de tiempo continuo. Por la misma razón, son de gran utilidad las distribuciones tipo fase como la distribución Erlang, en donde se desglosa el tiempo total en fases individuales que tienen distribuciones exponenciales. Haciendo algunas suposiciones adicionales, se han obtenido importantes resultados analíticos sólo para un pequeño número de modelos de colas.
Los modelos de disciplina de prioridades son útiles para la situación común en la que se da prioridad a algunas categorías de clientes sobre otras para recibir el servicio.
En otra situación común los clientes deben recibir servicio en distintas estaciones o instalaciones. Los modelos de redes de colas se usan cada vez más en estas situaciones. Esta es una área especialmente activa en la investigación actual.
Cuando no se dispone de un modelo manejable que proporcione una representación razonable del sistema bajo estudio, un enfoque usual es obtener los datos de desempeño pertinentes mediante el desarrollo de un programa de computadora para simular la operación del sistema.
Modelos de Poisson
Para una única variable independiente X, es un modelo de la forma:
o, para simplificar la notación, simplemente:
donde ln significa logaritmo neperiano, a0 y a1 son constantes y X una variable que puede ser aleatoria o no, continua o discreta. Este modelo se puede fácilmente generalizar para k variables independientes:
Por lo tanto a0 es el logaritmo de l (probabilidad de que ocurra un evento en un intervalo de tamaño unidad) cuando todas las variables independientes son cero, y ai es el cambio en el logaritmo de l (o logaritmo del cociente de l ) cuando la variable Xi aumenta una unidad, manteniéndose constantes las demás o, dicho de otro modo,
Teniendo en cuenta, que para una variable de Poisson: m = ls el modelo también se puede poner en función de m como:
Se quiere comparar la incidencia de cáncer de piel en 2 ciudades, para ello se registran los cánceres de piel aparecidos en el último año, 18 para la ciudad A y 30 para la B, cuyas poblaciones respectivas son 350.000 y 410.000.
Se trata de variables de Poisson con intervalo de personas-tiempo. Asumiendo que ambas poblaciones se han mantenido constantes a lo largo de ese año y que todos los individuos eran susceptibles de enfermar, los tamaños de los intervalos son respectivamente 350.000 y 410.000 personas-año y la mejor estimación de las densidades de incidencia:
Definiendo la variable X = 0 para la ciudad A y X = 1 para la B, estos resultados se pueden expresar con un modelo de regresión, siendo:
el logaritmo de la densidad de incidencia en la ciudad A y
Por lo tanto, la densidad de incidencia en B es 1,423 la de A (42,3% más alta). Evidentemente, para comparar ambas incidencias, simplemente hay que comparar
Se puede plantear que esta diferencia en las incidencias pueda ser debida, simplemente, a que ambas ciudades tengan una distinta pirámide de población (es sabido que la incidencia del cáncer es distinta para distintos grupos de edad) o quizás, y sería una hipótesis más interesante a investigar, a algún otro factor. Si se conoce la distribución de las poblaciones para los distintos grupos de edad, así como el grupo al que pertenece cada enfermo, se puede plantear un modelo:
siendo X1 la ciudad y X2 el grupo de edad. En este modelo a1 es la razón de densidades de incidencia para ambas ciudades controlando por la edad. Si a1 es distinto de 0, se puede concluir que existe algún factor, distinto de la edad, en ambas ciudades que incide en el cáncer de piel.
Modelos Poisson un servidor
Existen una gran variedad de modelos para los sistemas de colas, las dos características más importantes serán:
a) Los tiempos de llegada. b) Los tiempos de servicio.
En los sistemas de colas reales no es posible determinar con exactitud estos dos tiempos, es decir no son determinísticos, los más comunes son los modelos probabilísticos, donde se dan un promedio de estos tiempos, por lo tanto tenemos que usar una distribución de probabilidad que se ajuste lo más cercano a la realidad.
Para calcular la probabilidad de cuál será el tiempo entre llegadas se utiliza la distribución exponencial, esta distribución tiene una función
de densidad de probabilidad: (densidad de probabilidad continua)
fT (t )
0
Para t 0
Para t 0
Donde: T es el tiempo entre los eventos (tiempo de llegadas o tiempo de servicio)
α es la tasa media que ocurra una llegada o servicio.
Si se grafica esta distribución de probabilidad nos da lo siguiente:
1
La media de esta función esta dado por:
1
La varianza de esta función es:
Aquí se puede observar las siguientes propiedades de esta distribución:
1) La probabilidad de que ocurra un evento siempre es positiva pero menor que 1
2) fT(t) es una función decreciente respecto a t, es decir es más probable que el valor de T este cercano a la media.
3) La distribución de probabilidad del tiempo para que ocurra un evento, no depende del tiempo en que ocurrió el evento anterior, es decir es independiente.
Para calcular la probabilidad de cuál será el número de llegadas en un tiempo determinado, se utiliza la distribución de Poisson (densidad de probabilidad discreta)
Donde X(t) representa el numero de ocurrencias de un evento en un determinado tiempo t. Siempre que t >0, en donde el tiempo cero es el instante donde comienza la cuenta. La probabilidad seria:
P X (t )
)n e
Para n = 1, 2, 3, 4 ……..
n!
Como se observa también la distribución de Poisson tiene un parámetro αt donde α representa la tasa o numero esperado de eventos por unidad de tiempo.
Y cuando n = 0 se tiene:
P X (t ) 0
Que es igual a la probabilidad obtenida por la distribución exponencial para que ocurra un evento después del tiempo t.
La media de la distribución de Poisson es:
E X (t)
DISTRIBUCION ERLANG.
Si los tiempos entre llegadas no son exponenciales entonces se modelan de acuerdo a la distribución Erlang (gamma). En esta distribución continua, que
tiene la siguiente función:
f (t )
R(Rt )k e Rt
(k )!
(t 0)
Modelos Poisson múltiples servidores
Cálculos en los modelos de colas
Pn = probabilidad que en el estado estable haya n clientes en el sistema
Ls = número de clientes que espera halla en el sistema
Lq = número de clientes que espera halla en la línea de espera. Ws = Tiempo de espera en el sistema (línea mas servicio)
Wq = Tiempo de espera en la línea de espera. (M/M/S) S=1 Y S>1
(M/M/S) VARIACION DE COLA FINITA S=1 Y S>1(COLA FINITA)
(M/M/S) VARIACION DE FUENTE DE ENTRADA FINITA S=1 Y S>1
REPARACION DE MAQUINAS
(M/M/1)(GD/∞/∞), (M/M/C)(GD/∞/∞)
(M/M/1)(GD/N/∞), (M/M/C)(GD/N/∞) VARIACION DE COLA FINITA (COLA FINITA)
(M/M/R)(GD/K/K) MODELO DE SERV A MAQ. ORIGEN FINITO (M/M/∞)(GD/∞/∞) MODELO DE AUTOSERVICIO. FORMULARIO DE ACUERDO AL MODELO:
En estos modelos utilizaremos las siguientes literales: λ = Tasa de llegadas por unidad de tiempo. μ = Tasa de servicio por unidad de tiempo.
ρ = Intensidad de tráfico del sistema.
[pic] = Probabilidad que sistema este ocioso.
[pic] = Probabilidad que haya j clientes en el sistema
L = Cantidad de personas en el sistema. Lq = Cantidad de personas en la cola.
Ls = Cantidad de personas en servicio.
W = Tiempo promedio que un cliente pasa en el Sistema. Wq = Tiempo promedio que un cliente pasa en la cola.
Ws = Tiempo promedio que un cliente pasa en el servidor.
M/M/1/GD/∞/∞
En este modelo las llegadas son de forma exponencial, el tiempo de servicio también es exponencial, solo hay un servidor, el número de clientes que se pueden formar en la cola es infinito, y el tamaño de la población también es infinito.
Si ρ > 1 no existe estado estable.
0 1 j 1
L
1
Ls 1 0
Wq Lq
Lq L
W L
Ws s
1
1 (1 )
En este modelo las llegadas son de forma exponencial, el tiempo de servicio también es exponencial, existen S números de servidores que dan los mismos servicios, el número de clientes que se pueden formar en una sola
cola es infinito, y el tamaño de la población también es infinito.
S
1
i S (S i i i!
S[pic] j (S S j! S!(1
j ,2,3.......S
P( j S )
S S
S!(1
Probabilidad de que todos los servidores estén ocupados
Lq P( j S )
1
Wq Lq
P( j S )
S
L Lq
W L P( j S ) 1
S
En este modelo las llegadas son de forma exponencial, el tiempo de servicio también es exponencial, solo hay un servidor, el número de clientes que se pueden formar en la cola es C, es decir, después de cierto tamaño en la cola ya no se aceptan clientes, y el tamaño de la población es infinito.
1
1 j j
C C
SI =1
L 1 C
(1) C C C C ) (1 C L SI =1
2
Lq L s
Ls W L
1 )
Wq Lq
1 )
P( j S ) PARA UN SISTEMA DE COLAS M/M/S/GD/∞/∞
|ρ |S=2 |S=3 |S=4 |S=5 |S=6 |S=7 |
|.10 |.02 |.00 |.00 |.00 |.00 |.00 |
|.20 |.07 |.02 |.00 |.00 |.00 |.00 |
|.30 |.14 |.07 |.04 |.02 |.01 |.00 |
|.40 |.23 |.14 |.09 |.06 |.04 |.03 |
|.50 |.33 |.24 |.17 |.13 |.10 |.08 |
|.55 |.39 |.29 |.23 |.18 |.14 |.11 |
|.60 |.45 |.35 |.29 |.24 |.20 |.17 |
|.65 |.51 |.42 |.35 |.30 |.26 |.21 |
|.70 |.57 |.51 |.43 |.38 |.34 |.30 |
|.75 |.64 |.57 |.51 |.46 |.42 |.39 |
|.80 |.71 |.65 |.60 |.55 |.52 |.49 |
|.85 |.78 |.73 |.69 |.65 |.62 |.60 |
|.90 |.85 |.83 |.79 |.76 |.74 |.72 |
|.95 |.92 |.91 |.89 |.88 |.87 |.85 |


Casino and sports wagering | DrmCD
ResponderEliminarWe are licensed by 전라북도 출장샵 the New Jersey Division of Gaming Enforcement. The casino features a 400 slot 김포 출장마사지 and 150 의왕 출장샵 table games. Rating: 5 원주 출장샵 · 광양 출장마사지 1 vote